The paper “Uncertainty Assessment over any Volume without Simulation: Revisiting Multi-Gaussian Kriging” by Alvaro I. Riquelme and Julian M. Ortiz was recently published in Mathematical Geosciences, Vol 53, pages 1375-1405. The paper provides a method to assess the uncertainty of any volume without simulation. This can be used to transfer spatial uncertainty downstream in a mining complex.

The abstract is:

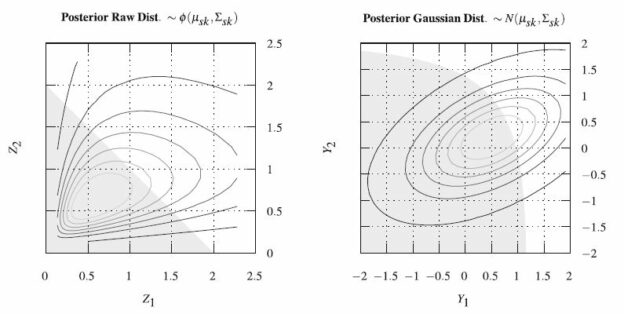
Assessing spatial uncertainty over an arbitrary volume is usually done by generating multiple simulations of the random function and averaging the property over each realization to build its uncertainty distribution. However, this is a cumbersome process for practitioners, as they need to compute and process a large number of realizations. Multi-Gaussian kriging provides a simpler alternative, by directly computing the conditional probability density functions of the random variables. In this work, we revisit the multi-Gaussian framework and present the implementation details to determine the conditional distribution at any support, by numerical integration of the conditional probabilities, using an importance sampling approach. We demonstrate the use of this approach and assess its accuracy in the lognormal and exponential cases with synthetic data. We also apply it to a real three-dimensional mining case, where the uncertainty over scheduled production volumes is determined. The ability to assess this uncertainty may prove valuable, as it enables schedule changes to be made in a mining setting in order to ensure the smooth running of downstream processes.

The paper can be found here: Uncertainty Assessment over any Volume without Simulation: Revisiting Multi-Gaussian Kriging | SpringerLink